Mathway

您可以信赖的解决方案！轻松应对数学挑战旨在帮助学生、教师和数学爱好者

付费

立即访问

详情

Mathway 解题步骤详解

Mathway 解题流程高度简化，无论是网页端还是移动端，均遵循 “输入问题→选择类型→获取解答→查看解析” 的核心逻辑，以下结合代数例题（以 “解一元二次方程 \(x^2 - 4x + 3 = 0\)” 为例），分步说明操作方法：

一、准备：进入对应解题板块

打开 Mathway 官网（https://www.ma thwa y .com/），在顶部导航栏选择需解决的数学领域，如 “Algebra（代数）”；若直接访问代数板块（https://www.mathw ay.co m/Alg ebra），可跳过此步。

移动端需先打开 Mathway 应用，首次使用需允许必要权限（如拍照权限，用于拍照解题），再在首页选择 “Algebra” 分类。

二、第一步：输入待解问题

Mathway 提供两种主流输入方式，可根据问题形式选择：

1. 手动输入（适用于文字描述或公式类问题）

点击页面中央的 “Enter a problem...” 输入框，会弹出数学符号键盘（含平方、根号、等号、括号等）。

以 “\(x^2 - 4x + 3 = 0\)” 为例：

① 输入 “x”，点击符号键盘的 “²”（生成 “\(x^2\)”）；

② 输入 “-4x+3=”，最后输入 “0”，完成公式输入。

若问题为文字描述（如 “求 2x + 5 = 15 中 x 的值”），可直接用中文或英文输入文字，AI 会自动识别并转化为数学表达式。

2. 拍照识别（适用于纸质 / 屏幕上的印刷体题目，仅移动端支持）

在移动端 Algebra 板块点击 “相机” 图标，对准待解题目，确保题目清晰、无遮挡（建议仅拍摄单道题，避免多题干扰识别）。

点击拍照按钮后，系统会自动识别题目内容，生成对应的数学公式（如识别纸质上的 “\(x^2 - 4x + 3 = 0\)”），若识别有误，可手动在预览页修改。

三、第二步：选择解题目标（明确需求）

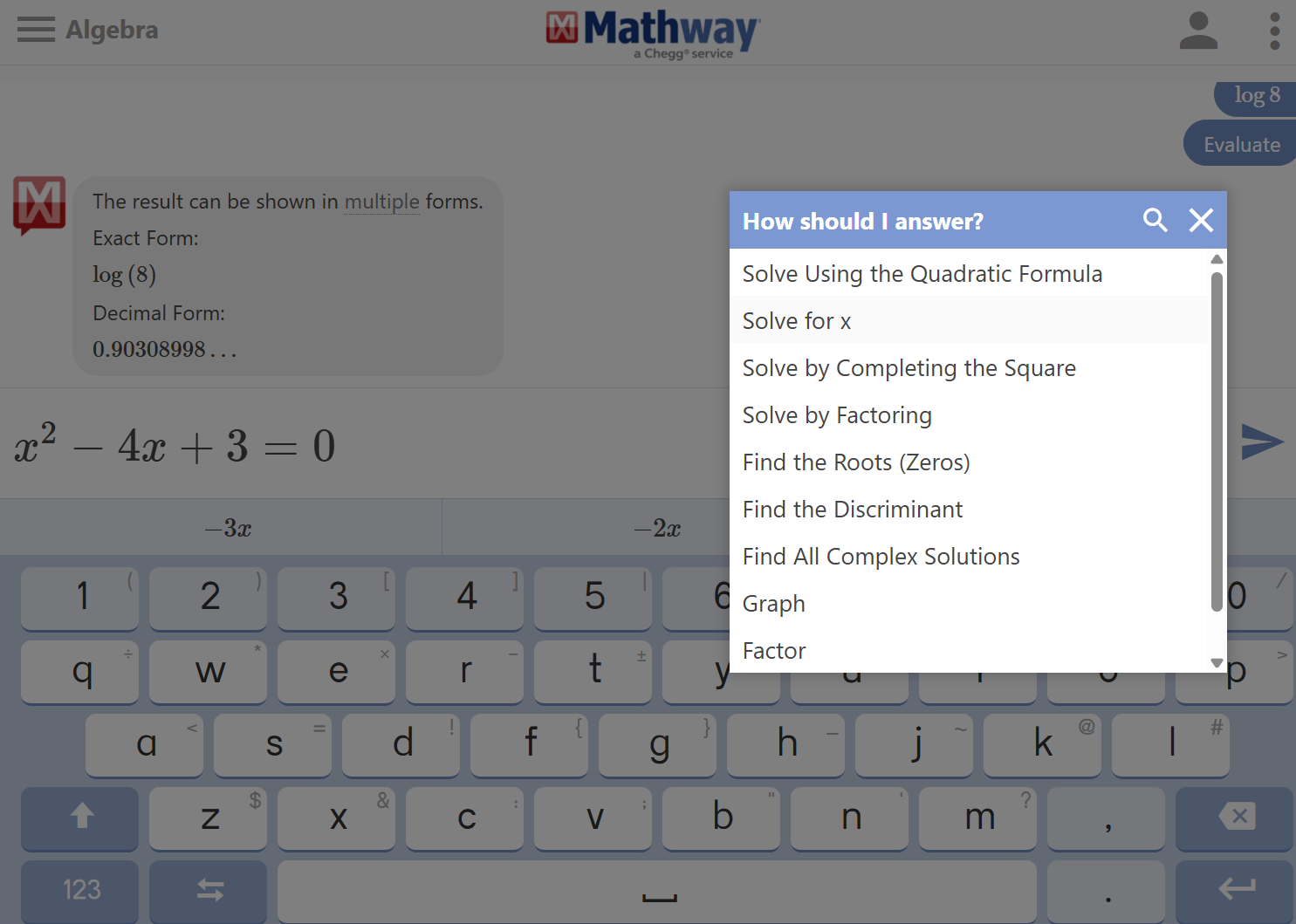
输入问题后，需选择具体的 “解题类型”，确保工具理解你的需求：

页面会自动弹出选项列表（如 “Solve for x”“Factor”“Graph” 等），根据问题选择对应目标。

以 “\(x^2 - 4x + 3 = 0\)” 为例，选择 “Solve for x（求解 x）”；

若问题是 “因式分解 \(x^2 - 4x + 3\)”，则选择 “Factor”；若需画函数图像，选择 “Graph”。

部分复杂问题（如方程组 “2x + y = 7，x - y = 1”），输入后需选择 “Solve the system of equations”（解方程组）。

四、第三步：获取解题结果与分步解析

1. 免费用户：查看基础结果

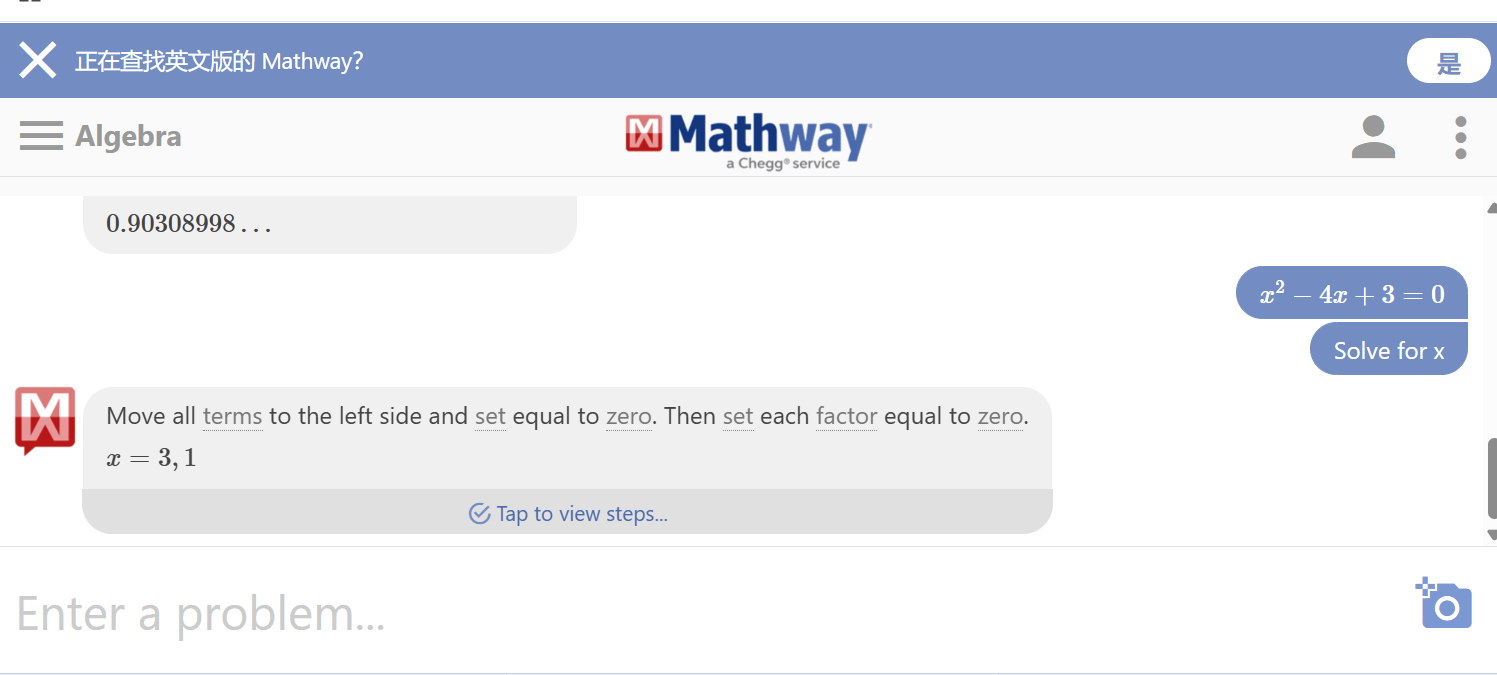
点击 “Submit”（提交）按钮，系统会在 1-3 秒内生成最终答案（如 “\(x = 1\) 或 \(x = 3\)”）。

免费用户可直接获取答案，但无法查看完整分步过程，仅能看到 “Upgrade to see step-by-step explanation”（升级后查看分步解析）的提示。

2. 付费用户 / 试用用户：查看完整分步解析

若已订阅或处于 7 天免费试用期间，提交后会自动显示分步解题过程，以 “\(x^2 - 4x + 3 = 0\)” 为例：

① 第一步：因式分解二次三项式

“\(x^2 - 4x + 3 = (x - 1)(x - 3)\)”（说明：寻找两个数，使其乘积为 3、和为 -4，即 -1 和 -3）；

② 第二步：应用 “因式分解法解一元二次方程” 规则

“若 \((x - 1)(x - 3) = 0\)，则 \(x - 1 = 0\) 或 \(x - 3 = 0\)”；

③ 第三步：求解单变量方程

“由 \(x - 1 = 0\) 得 \(x = 1\)；由 \(x - 3 = 0\) 得 \(x = 3\)”；

④ 第四步：总结答案

“方程的解为 \(x = 1\) 和 \(x = 3\)”。

部分问题（如函数图像题）还会附带可视化图表，标注关键点（如二次函数的顶点、对称轴）。

五、第四步：后续操作（可选）

修改问题：若对结果有疑问或输入有误，点击输入框旁的 “Edit”（编辑）按钮，重新修改问题后再次提交。

保存 / 分享：付费用户可将解题过程保存至个人账号（“Save” 按钮），或通过链接、截图分享给他人（如同学、老师）。

拓展学习：部分题目会附带相关知识点提示（如 “一元二次方程的解法”），点击可跳转至简要讲解，辅助理解解题原理。

注意事项

输入准确性：手动输入时需注意符号正确性（如 “\(x^2\)” 勿输为 “x2”），拍照时需避免光线过暗、文字模糊，否则可能影响识别准确率。

解题类型匹配：若选择错误的解题目标（如将 “解方程” 误选为 “因式分解”），会导致结果不符合需求，需重新选择后提交。

权限与网络：移动端拍照解题需开启相机权限，所有操作需联网，确保工具能实时调用 AI 计算能力。